Digital Imaging Tutorial

3. Conversion

Key Concepts

introduction
scanning factors
rich digital master
benchmarking
text
stroke
continuous-tone halftone
proposed method guidelines

additional reading

BENCHMARKING FOR DIGITAL CAPTURE
Cornell advocates a methodology for determining conversion requirements that is based on the following:

Assessing document attributes (detail, tone, color)
Defining the needs of current and future users
Objectively characterizing relevant variables (e.g., size of detail, desired quality, resolving power of system)
Correlating variables to one another via formulas
Confirming results through testing and evaluation

BENCHMARKING RESOLUTION REQUIREMENTS FOR PRINTED TEXT
Cornell adopted and refined a digital Quality Index (QI) formula for printed text that was developed by the C10 Standards Committee of AIIM. (An explanation of this approach is found in: Tutorial: Determining Resolution Requirements for Reproducing Text-based Material). This formula was based on translating the Quality Index method developed for preservation microfilming standards to the digital world. The QI formula for scanning text relates quality (QI) to character size (h) in mm and resolution (dpi). As in the preservation microfilming standard, the digital QI formula forecasts levels of image quality: barely legible (3.0), marginal (3.6), good (5.0), and excellent (8.0).

Table: Metric/English Conversion

...1 mm = .039 inches
...1 inch = 25.4 mm

The formula for bitonal scanning provides a generous over sampling to compensate for misregistration and reduced quality due to thresholding information to black and white pixels.

Bitonal QI Formula for Printed Text
QI = (dpi x .039h)/3
h = 3QI/.039dpi
dpi = 3QI/.039h

Note: if the measurement of h is expressed in inches, omit the .039.

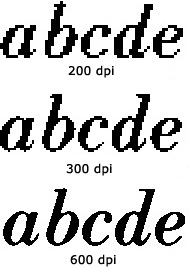
Resolution Requirements For Printed Text: Comparison of letters scanned at different resolutions.

Some printed text will require grayscale or color scanning for the following reasons:

Pages are badly stained
Paper has darkened to the extent that it is difficult to threshold the information to pure black and white pixels
Pages contain complex graphics or important contextual information (e.g., embossments, annotations)
Pages contain color information (e.g., different colored inks)

Scanning Text: Compare bitonal (left) and grayscale (right) scanning of a stained text page.

Because tonal images subtly "gray out" pixels that are only partially on a stroke, a separate formula was developed for grayscale/color scanning of printed text:

Grayscale/Color QI Formula for Printed Text
QI = (dpi x .039h)/2
h = 2QI/.039dpi
dpi = 2QI/.039h

Note: if the measurement of h is expressed in inches, omit the .039.

Example: The Case of the Brittle Book

Cornell used benchmarking to determine conversion requirements for brittle books containing text and simple graphics, such as line art, charts, diagrams, and the like. Although some of the books contained darkened pages, in most cases the contrast between text and background was sufficient for capturing text in bitonal mode. We determined resolution requirements by assessing the level of detail and by defining our quality needs.

Printed text offers a fixed metric for detail: the height of the smallest significant lowercase letter. In a review of commercial typescripts commonly used from 1850-1950, Cornell discovered that virtually no publishers used fonts shorter than 1 mm in height. We were interested in creating paper replacements for the deteriorating originals, so our quality requirement was high--we wanted excellent rendering of the fonts, including full representation of the serifs and other attributes.

Once we had determined the size of the detail and the desired quality, our next step was to equate those requirements to the necessary resolution. Using the bitonal QI formula, and a fixed detail metric of 1mm, Cornell predicted that textual information could be captured with excellent quality at a resolution of 600 dpi. An extensive onscreen and print examination of digital facsimiles for a range of typescripts used during the brittle book period confirmed these benchmarks. Although many of the books did not contain such small text, to avoid an item-by-item review, all books are scanned at 600 dpi.

Reality Check

Calculate the bitonal scanning resolution required to achieve excellent quality (QI = 8) for a 3 mm high character. (Round to nearest whole number.)

When using a 400 dpi bitonal scanner, what would be the size of the smallest character that you could capture with medium quality (QI=5)? (Round your answer to the nearest hundredth of a millimeter.)